Угол давления зубчатого колеса что это

Опубликовано: 21.04.2024

Ни один хороший механизм не может быть построен без такой детали, как зубчатое колесо (или, иначе, шестерня). Правильное понимание того, как шестерни влияют на такие параметры, как крутящий момент и скорость вращения, очень важно. Ниже будет рассказано об азах зубчатых передач и о том, как правильно их использовать.

Механическое преимущество: крутящий момент против скорости вращения

Зубчатые передачи работают по принципу механического преимущества. Это значит, что с помощью использования шестерен различных диаметров вы можете изменять скорость вращения выходного вала и вращающий момент, развиваемый приводным двигателем.

Любой электродвигатель имеет определенную скорость вращения и соответствующий его мощности крутящий момент. Но, к сожалению, для многих механизмов предлагаемые на рынке и подходящие по стоимости асинхронные двигатели обычно не обладают желаемым соотношением между скоростью и моментом (исключением являются сервоприводы и мотор-редукторы с высоким моментом). Например, вы действительно хотите, чтобы колеса вашего робота-уборщика вращались со скоростью 3000 об/мин при низком крутящем моменте? Нет конечно, поэтому последний зачастую предпочтительнее скорости.

Уравнение зубчатой передачи

Она обменивает высокую входную скорость на больший выходной крутящий момент. Этот обмен происходит по очень простому уравнению, которое можно записать так:

Момент _{входной} * Скорость _{входная} = Момент _{выходной} * Скорость _{выходная}

Скорость входную можно найти, просто просматривая табличку приводного электродвигателя. Момент входной легко определить по этой скорости и механической мощности из той же таблички. Затем просто подставим выходную скорость или требуемый крутящий момент в правую часть уравнения.

Например, предположим, что ваш асинхронный двигатель при моменте на выходном валу 0,5 Н∙м имеет скорость 50 об/с, но вы хотите только 5 об/с. Тогда ваше уравнение будет выглядеть так:

0,5 Н∙м * 50 об/с = Момент _{выходной}* 5 об/с.

Ваш выходной крутящий момент будет 5 Н∙м.

Теперь предположим, что с тем же мотором вам нужно 5 Н∙м, но при этом требуется минимальная скорость 10 об/с. Как бы узнать, способен ли на это ваш мотор вместе с зубчатой передачей (т. е., по сути, мотор-редуктор)? Обратимся снова к нашему уравнению

0,5 Н∙м * 50 об/с = 5 Н∙м * Скорость _{выходная},

Скорость _{выходная} = 5 об/с.

Итак, вы определили, используя простое уравнение, что при показателе Момент _{выходной} =5 Н∙м обеспечить скорость выходную в 10 об/с ваша зубчатая передача не способна. Вы только что сохранили себе кучу денег, так как не потратили их на механизм, который никогда не заработал бы.

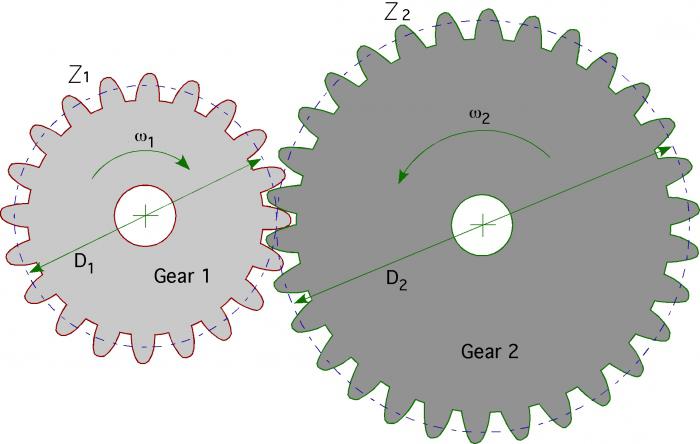
Передаточное число зубчатой передачи

Мы записали уравнения, но как механически поменять местами крутящий момент и скорость? Для этого нужны две шестерни (иногда больше) различных диаметров, чтобы иметь конкретное передаточное число. В любой паре шестерен большее зубчатое колесо будет двигаться более медленно, чем меньшее, но оно будет передавать на выходной вал больший крутящий момент. Таким образом, чем больше величина разницы (или передаточное число) между двумя колесами, тем больше разница их скоростей и передаваемых крутящих моментов.

Передаточное число показывает, во сколько раз зубчатая передача изменяет скорость и вращающий момент. Для него, опять же, имеется очень простое уравнение.

Предположим, что передаточное число равно 3/1. Это будет означать, что вы увеличиваете ваш крутящий момент втрое, а скорость втрое снижаете.

Момент _{входной} = 1,5 Н∙м, Скорость _{входная} = 100 об/с,

Передаточное число = 2/3

Момент _{выходной} = Момент _{входной} * 2/3 = 1 Н∙м,

Скорость _{выходная} = Скорость _{входная} * 3/2 = 150 об/с.

Итак, на выходе передачи момент в полтора раза вырос, а скорость точно так же снизилась.

Достижение определенного передаточного числа

Если вы хотите достичь простой его величины, скажем 2 к 1, вы должны использовать две шестерни, одна из которых вдвое больше другой. Это не что иное, как отношение их диаметров. Если диаметр зубчатого колеса в 3 раза больше, чем у сцепленного с ним другого, то вы получите передаточное число 3/1 (или 1/3).

Для гораздо более точного способа вычислить передаточное число подсчитайте отношение зубьев на шестернях. Если одна из них имеет 28 зубьев и другая - 13, вы получите передаточное число 28 / 13 = 2,15 или 13 / 28 = 0,46. Подсчет зубьев всегда будет давать вам наиболее точную величину.

Эффективность передач

К сожалению, в зубчатой передаче вы имеете определенные энергетические потери. Это обусловлено очевидными причинами, такими как трение, рассогласование углов давления, смазкой, зазорами (расстоянием между сцепленными зубьями двух шестерен), а также угловыми моментами и т. д. Различные типы передач, разные виды зубчатых колес, различные материалы и износ шестерен, – все это будет влиять на КПД передачи. Возможные их комбинации дадут слишком большой список, поэтому точную величину КПД передачи, которые вы используете, вы сможете найти в документации на нее.

Предположим, что вы используете два цилиндрических зубчатых колеса. Обычное КПД такой передачи примерно

90%. Умножьте это число на вашу скорость выходную и момент выходной, чтобы получить истинные выходные величины передачи.

Если (из предыдущего примера):

Передаточное число = 2/3

Момент _{выходной} = Момент _{входной} * 2/3 = 1 Н∙м,

Скорость _{выходная} = Скорость _{входная} * 3/2 = 150 об/с,

Истинный Момент _{выходной} = 1 Н∙м * 0,9= 0,9 Н∙м,

Истинная Скорость _{выходная} = 150 об/с * 0,9 = 135 об/с.

Направление вращения шестерен

Разрабатывая любую зубчатую передачу, нужно понимать, как она изменяет направление вращения выходного вала. Две сцепленные шестерни всегда будут вращаться в противоположных направлениях. Это означает, что если одна вращается по часовой стрелке, то другая всегда будет вращаться против нее. Это вполне очевидно. Но что делать, если у вас есть передача, скажем, из шести сцепленных шестерен? Правило здесь следующее: входной и выходной валы у передач с нечетным числом шестерен всегда вращаются в одном направлении, а при четном числе шестерен – в противоположном.

Конструкция и параметры зубчатого колеса

Оно содержит венец с зубьями, диск и ступицу. Имеется три наиболее важных его параметра: модуль, диаметр делительной окружности и количество зубьев. Какую же делительную окружность имеет зубчатое колесо? Чертеж цилиндрического колеса с типовыми эвольвентными зубьями показан ниже.

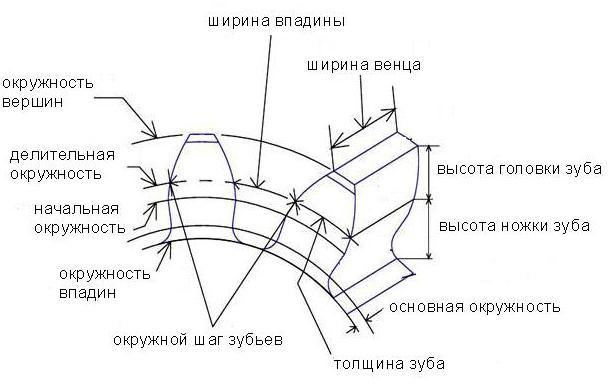
Например, зубчатое колесо с 22 зубьями и диаметром 44 мм имеет модуль m = 2 мм. Сцепленные шестерни должны обе иметь один модуль. Значения их стандартизованы, и как раз на делительной окружности модуль данного колеса принимает свое стандартное значение.

Высота головки зуба одного колеса меньше высоты ножки зуба второго, зацепляющегося с ним, благодаря чему образуется радиальный зазор c.

Для обеспечения бокового зазора δ между двумя сцепленными зубьями сумма их толщин принимается меньше их окружного шага p. Радиальный и боковой зазоры предусматриваются для создания необходимых условий смазки, нормальной работы передачи при неизбежных неточностях изготовления и сборки, тепловом увеличении размеров передачи и т. п.

Расчет зубчатого колеса

Он всегда ведется в составе расчета конкретной зубчатой передачи. Исходными данными для него обычно являются мощность (или крутящий момент), угловые скорости (или скорость одного вала и передаточное число), условия работы (характер нагрузки) и срок службы передачи.

Дальнейший порядок относится к закрытой цилиндрической прямозубой передаче.

1. Определение передаточного числа u.

2. Выбор материалов колес в зависимости от условий работы, назначение термообработки и значения твердости рабочих поверхностей зубьев.

3. Расчет зубьев передачи на изгиб.

4. Расчет зубьев передачи на контактную прочность (прочности контактирующих поверхностей зубьев).

5. Определение межосевого расстояния a_W из условия контактной прочности и округление его значения до стандартного.

6. Задание модуля из соотношения m = (0,01 - 0,02) х a_W и округление его значения до ближайшего стандартного. При этом в силовых передачах желательно иметь m ≥1,5 – 2 мм.

7. Определение суммарного числа зубьев передачи, числа зубьев шестерни и колеса.

8. Выбор коэффициентов формы зубьев для шестерни и колеса.

9. Проверка прочности зубьев по напряжениям изгиба.

10. Проведение геометрического расчета передачи.

11. Определение окружной скорости колеса и назначение соответствующей точности зацепления.

Расчет зубчатого колеса в составе открытой зубчатой передачи несколько отличается от приведенного, но в основном последовательность его такая же.

Как обозначается точность изготовления зубчатых колес

При изготовлении любые их виды имеют ряд погрешностей, среди которых выделяют четыре основные:

кинематическую погрешность, связанную в основном с радиальным биением зубчатых венцов;
погрешность плавности работы, вызываемую отклонениями шага и профиля зубьев;
погрешность контакта зубьев в передаче, которая характеризует полноту прилегания их поверхностей в зацеплении;
боковой зазор между неработающими поверхностями зубьев.

Для контроля первых трех погрешностей стандартами установлены специальные показатели – степени точности от 1 до 12, причем точность изготовления увеличивается с уменьшением показателя. Для контроля четвертой погрешности изготовления имеются два показателя:

вид сопряжения зубчатых колес – обозначается литерами A, B, C, D, E, H;
допуск на боковой зазор – обозначается литерами x, y, z, a, b, c, d, e, h.

Для обоих показателей бокового зазора обозначения даны в порядке убывания его величины и допуска на него.

Условно точность зубчатых колес обозначается двумя способами. Если степень точности по первым трем погрешностям одинакова, то ставится один общий для них численный показатель степени точности, за которыми стоят литеры обозначения вида сопряжения и допуска на боковой зазор. Например:

8-Ас ГОСТ 1643 – 81.

Если точности по первым трем погрешностям разные, то в обозначении ставятся три численных показателя последовательно. Например:

5-4-3-Са ГОСТ 1643 – 81.

Типы зубчатых передач

Любое зубчатое колесо, независимо от его типа, делается и работает по одним и тем же вышеприведенным принципам. Однако различные их типы позволяют выполнить разные задачи. Некоторые виды передач обладают или высоким КПД, или высоким передаточным отношением, или же работают с непараллельными осями вращения шестерен, к примеру. Ниже приведены основные общие типы. Это не полный список. Также возможно и сочетание нижеприведенных типов.

Примечание: Приведены только типичные КПД передач. Из-за многих других возможных факторов приводимые КПД должны использоваться только в качестве справочных величин. Часто производители приводят ожидаемые КПД в паспортах для своих передач. Помните, что износ и смазка будут также существенно влиять на эффективность передач.

Цилиндрические прямозубые колеса (КПД

Цилиндрическое зубчатое колесо имеет зубья, расположенные на цилиндрической поверхности. Передачи с ними являются наиболее часто используемыми типами благодаря своей простоте и максимальной эффективности среди всех других. Передаточное число для одной пары u ≤ 12,5. Не рекомендуется для очень высоких нагрузок, так как прямые зубья зубчатого колеса довольно легко ломаются.

Цилиндрические косозубые колеса (КПД

Они работают так же, как цилиндрические прямозубые, для передачи момента между параллельными валами, но у такой передачи более плавно происходит зацепление. Вследствие этого они создают меньше шума при работе и имеют меньшие габариты. У них большая нагрузочная способность. К сожалению, из-за сложной формы зубьев они, как правило, более дорогие.

Цилиндрические шевронные колеса

Являются разновидностью предыдущего вида. Чем отличается такое зубчатое колесо. Чертеж его показан ниже. Видно, что по ширине его венца расположены зубья с правым и левым наклоном, так что такие составные зубья зубчатого колеса по форме напоминает «шевроны». Эти колеса обладают всеми преимуществами косозубого их вида, плюс отсутствием осевых нагрузок. Они способны самоцентрироваться и не нуждаются в дорогостоящих радиально-упорных подшипниках для восприятия осевых нагрузок.

Конические зубчатые колеса (КПД

Зубья этих колес, располагающиеся на конических поверхностях, выполняют прямыми, косыми, круговыми (дугообразными). Эти передачи применяют для передачи момента между перекрещивающимися под разными углами валами. К сожалению, их КПД довольно низок, поэтому следует избегать их применения, если возможно.

Червячные передачи (КПД

Это передача с винтом-червяком на одном валу и червячным колесом на втором, перпендикулярном первому, валу. Они имеют очень высокое передаточное число. В расчетах принимают во внимание то, что у червяка (однозаходного) имеется только один зуб (виток).

Углом давления ? называется угол между вектором силы действующей на ведомое звено с ведущего и вектором скорости точки приложения этой силы на ведомом звене.

Ведущим звеном называется звено, для которого работа внешнич сил приложенным к нему положительна, ведомым – отрицательна или равна нулю.

Эвольвентная зубчатая передача - цилиндрическая зубчатая передача, профили зубьев которой выполнены по эвольвенте окружности.

Геометрические параметры эвольвентного зубчатого колеса

Эвольвентным зубчатым колесом называют звено зубчатого механизма, снабженное замкнутой системой зубьев.

При проектировании зубчатого колеса вначале нужно определить его число зубьев z, а затем определить параметры зубьев. Для этого нужно произвольную окружность колеса r_y разделить на z частей, каждая из которых называется окружным шагом p_y, где m_y= p_y/? = d_y/ z - модуль зацепления по окружности произвольного радиуса.

Модулем зацепления называется линейная величина в ? раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к ?.

В зависимости от окружности, по которой определен модуль, различают делительный, основной, начальный. Для косозубых колес еще и нормальный, торцевой и осевой модули.

В ряде стран используется величина обратная модулю, которая называется питчем. Питч (диаметральный) - число зубьев колеса, приходящееся на дюйм диаметра. Исходя из этого, модуль можно определить как число миллиметров диаметра, приходящееся на один зуб. На колесе можно провести бесчисленное число окружностей, на каждой из которых будет свой модуль.

Стандартной модуль определяется по окружности называемой делительной . Делительной называется такая окружность зубчатого колеса, на которой модуль и шаг принимают стандартное значение . Делительная окружность делит зуб на головку и ножку.

Примечание: Согласно ГОСТ основные элементы зубчатого колеса обозначаются по следующим правилам: линейные величины - строчными буквами латинского алфавита, угловые - греческими буками; установлены индексы для величин:

по окружностям: делительной - без индекса, вершин - a , впадин - f , основная - b , начальная - w , нижних точек активных профилей колес - p , граничных точек - l ;

по сечениям: нормальное сечение - n , торцевое сечение - t , осевое сечение - x ;

относящихся к зуборезному инструменту - 0 .

Окружность вершин (r_a) - очерчивает вершины зубьев ., где- коэффициент высоты головки зуба.

Окружность впадин (r_f) - очерчивает ножки зубьев.,

где - коэффициент высоты ножки зуба.

Основная окружноcть (r_b) – это окружность, по которой перекатывается нормаль .

Окружным шагом или шагом называется расстояние по дуге окружности между одноименными точками профилей соседних зубьев (под одноименными понимаются правые или левые профили зуба).

Угловой шаг ? - центральный угол, соответствующий дуге p - окружному шагу.

Углом профиля ? называется острый угол между касательной к профилю в данной точке и радиусом - вектором, проведенным в данную точку из центра колеса.

Шаг колеса делится на толщину зуба s_y и ширину впадины e_y.

Толщина зуба s_y - расстояние по дуге окружности r_y между разноименными точками профилей зуба.

Ширина впадины e_y - расстояние по дуге окружности r_y между разноименными точками профилей соседних зубьев.

В зависимости от соотношения между толщиной зуба и шириной впадины на делительной окружности зубчатые колеса делятся на:

нулевые s = e ; положительные s > e ; отрицательные s < e .

Общие термины, определения и обозначения

Gears.
General terms, definitions and symbols

Дата введения 1984-01-01

Постановлением Государственного комитета СССР по стандартам от 31 января 1983 г. N 557 дата введения установлена с 01.01.84

ПЕРЕИЗДАНИЕ. Ноябрь 2004 г.

Настоящий стандарт устанавливает применяемые в науке, технике и производстве термины, определения и обозначения основных понятий, относящихся к геометрии и кинематике зубчатых передач с постоянным передаточным отношением и являющихся общими для передач различных видов.

Термины и обозначения, установленные настоящим стандартом, обязательны для применения в документации всех видов, научно-технической, учебной и справочной литературе.

Стандарт полностью соответствует СТ СЭВ 3295-81.

Для каждого понятия установлен один стандартизованный термин. Применение терминов-синонимов стандартизованного термина запрещается.

Для отдельных стандартизованных терминов в стандарте приведены в качестве справочных краткие формы, которые разрешается применять в случаях, исключающих возможность их различного толкования. Установленные определения можно, при необходимости, изменять по форме изложения, не допуская нарушения границ понятий.

В случаях, когда необходимые и достаточные признаки понятия содержатся в буквальном значении термина, определение не приведено.

В стандарте приведен алфавитный указатель содержащихся в нем терминов и алфавитные указатели обозначений на основе латинского и греческого алфавитов.

В стандарте имеется приложение, содержащее простые индексы и правила построения сложных индексов обозначений параметров и элементов зубчатых передач.

Стандартизованные термины набраны полужирным шрифтом, их краткая форма - светлым.

ТЕРМИНЫ, ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ

1. Понятия, относящиеся к зубчатому колесу

1.1. Исходные понятия

Выступ на звене для передачи движения посредством взаимодействия с соответствующими выступами другого звена.

1.1.2. Зубчатое звено

Звено, имеющее один или несколько зубьев

1.1.3. Зубчатое колесо

Зубчатое звено с замкнутой системой зубьев, обеспечивающее непрерывное движение другого зубчатого звена (черт.2)

1.1.4. Зубчатый сектор

Зубчатое звено, представляющее собой сектор зубчатого колеса.

Примечание. Далее термины, относящиеся к зубчатому сектору, не приводятся; их следует строить аналогично терминам, относящимся к зубчатому колесу, с заменой слова "колесо" на слово "сектор", например, "ось зубчатого сектора" (черт.1) вместо "ось зубчатого колеса".

1.1.5. Секторное зубчатое колесо

Воображаемое зубчатое колесо, частью которого является зубчатый сектор (черт.1)

1.1.6. Число зубьев зубчатого колеса (секторного зубчатого колеса)

1.1.7. Число зубьев зубчатого сектора

Число зубьев сектора

Число зубьев, расположенных на зубчатом секторе.

1.1.8. Угол зубчатого сектора

Максимально возможный угол поворота зубчатого сектора при взаимодействии с зубчатым колесом (черт.2).

1.1.9. Ось зубчатого колеса

Геометрическая ось вращения зубчатого колеса в передаче

1.2. Объемные элементы зубчатого колеса

1.2.1. Тело зубчатого колеса

Часть зубчатого колеса, которая вместе с зубьями образует зубчатое колесо (черт.3)

1.2.2. Зубчатый венец

Часть зубчатого колеса, содержащая все зубья, связанные друг с другом прилегающей к ним поверхностью тела зубчатого колеса (черт.3)

1.2.3. Впадина

Пространство между соседними зубьями зубчатого колеса, ограниченное поверхностями вершин и впадин

1.3. Поверхности и сечения зубчатого колеса

1.3.1. Соосная поверхность зубчатого колеса

Поверхность вращения, ось которой совпадает с осью зубчатого колеса

1.3.2. Делительная поверхность зубчатого колеса

Соосная поверхность зубчатого колеса, которая является базой для определения элементов зубьев и их размеров.

1.3.3. Однотипная соосная поверхность зубчатого колеса

Однотипная соосная поверхность

Соосная поверхность зубчатого колеса одной формы с его делительной поверхностью (черт.4)

Примечание. Однотипными соосными поверхностями являются: цилиндрическая - для цилиндрической делительной поверхности; коническая - для конической делительной поверхности (при условии одностороннего относительно зубчатого колеса расположения вершин конусов);

тороидная - для тороидной делительной поверхности и т.д.

1.3.4. Поверхность впадин зубчатого колеса

Соосная поверхность, отделяющая зубья от тела зубчатого колеса (черт 5).

1.3.5. Поверхность вершин зубьев зубчатого колеса

Соосная поверхность, ограничивающая зубья со стороны, противоположной телу зубчатого колеса (черт.5)

1.3.6. Торец зубчатого венца

Одна из поверхностей, ограничивающих ширину зубчатого венца (черт.6)

1.3.7. Торец зуба

Часть торца зубчатого венца, принадлежащая зубу (черт.7)

1.3.8. Торцовое сечение зубчатого колеса

Сечение зубчатого колеса плоскостью, перпендикулярной к его оси, или соосной конической поверхностью, образующая которой нормальна к образующей делительной или начальной поверхности конического зубчатого колеса конической передачи (черт.8).

Примечание. При отсутствии указаний торцовое сечение соответствует делительной поверхности конического зубчатого колеса.

Перемещение функции непосредственного управления орудиями от человека к машине с помощью механических передач ознаменовало собой не просто техническую революцию – такие революции «местного значения» происходят в технике в связи с любым крупным изобретением. Нет, произошел полный переворот во всей технической системе, после которого она начала развиваться по-новому, на основании новых принципов, новых технических форм и структур. Иными словами, возникновение машин определило начало нового исторического этапа в развитии техники – механизации производства.

Необходимость изобретать и применять в промышленных масштабах различного рода машины невольно породила потребность в специалистах, способных осуществлять эту деятельность не от случая к случаю, а постоянно. Таким образом, переворот в техническом компоненте производительных сил привел к видоизменению человеческого компонента – появились инженеры механики. Проектирование передач инженерами осуществляется не только в соответствии с отечественной нормативной базой (ГОСТ, ОСТ), но и по стандартам других стран (AGMA, ASA, DIN, ISO, JIS, GBT). Применение зарубежных стандартов при проектировании механических передач расширяет возможности по ремонту импортных узлов и агрегатов, при этом способствует сокращению сроков и снижению цены ремонта сложного технологического оборудования.

Инженеры вовлечены, как правило, во все процессы жизненного цикла технических устройств и механических передач, являющихся предметом инженерного дела, включая прикладные исследования, планирование, проектирование, конструирование, разработку технологии изготовления, подготовку технической документации, производство, наладку, испытание, эксплуатацию, техническое обслуживание, ремонт и утилизацию.

Хороший инженер умеет почти всё. Он - технолог, механик, слесарь, наладчик. Как же это у него получается? На самом деле одна из основ знаний и умений инженера - это "глубина понимания". Вторая основа - опыт. В хороших ВУЗах инженеров учат не "знать всё на свете", а находить нужную информацию в кратчайшие сроки. С опытом приходит и умение "отделять мух от котлет" и "видеть" решение той или иной задачи/проблемы. Инженеру не составит большого труда разобраться в кинематической схеме оборудования, из каких передач оно состоит.

Механическая энергия, используемая для приведения в движение машины-орудия, представляет собой энергию вращательного движения вала двигателя. Вращательное движение получило наибольшее распространение в механизмах и машинах, так как обладает следующими достоинствами: обеспечивает непрерывное и равномерное движение при небольших потерях на трение; позволяет иметь простую и компактную конструкцию передаточного механизма.

Все современные двигатели для уменьшения габаритов и стоимости выполняют быстроходными с весьма узким диапазоном изменения угловых скоростей. Непосредственно быстроходный вал двигателя соединяют с валом машины редко (вентиляторы и т. п.). В абсолютном большинстве случаев режим работы машина-орган не совпадает с режимом работы двигателя, поэтому передача механической энергии от двигателя к рабочему органу машины осуществляется с помощью различных передач.

Передачей будем называть устройство, предназначенное для передачи энергии из одной точки пространства в другую, расположенную на некотором расстоянии от первой.

В современном машиностроении в зависимости от вида передаваемой энергии применяют механические, пневматические, гидравлические и электрические передачи.

Механическими передачами, или просто передачами, называют механизмы для передачи энергии от машины-двигателя к машине-исполнительному механизму, как правило, с преобразованием скоростей, моментов, а иногда — с преобразованием видов (например, вращательное в поступательное) и законов движения.

Передача (в механике) соединяет вал источника энергии - двигателя и валы потребителей энергии - рабочих органов машины, таких, например, как шпиндель токарного станка, ведущие колёса гусеничной техники или привод автомобиля.

Механические передачи известны со времен зарождения техники, прошли вместе с ней длительный путь развития и совершенствования и имеют сейчас очень широкое распространение. Грамотная эксплуатация механических передач требует знания основ и особенностей их проектирования и методов расчетов.

Сегодня я бы хотел более подробно раскрыть тему зубчатых механических передач и их предназначение в устройствах и узлах.

Что такое шестеренки?

Шестерня - это колесо с зубьями по окружности. Зубчатые передачи с одинаковым профилем зубьев зацепляются. Это позволяет передавать мощность с ведущего вала на ведомый. Шестерни обычно используются в тандеме из двух или более, используемых для передачи вращения от оси одной шестерни к оси другой.

Зубья шестерни на одной оси зацепляются с зубьями шестерни на другой, создавая таким образом связь между вращением двух осей. Когда одна ось вращается, другая тоже будет вращаться. Шестеренки также могут использоваться для перекачивания жидкостей, как, например, в случае шестеренчатых насосов для жидкого топлива и смазочного масла. Они настолько хорошо зацепляются (образуя поршневой насос прямого действия), что жидкость продвигается вперед с высоким давлением нагнетания. Они также используются в цепных блоках для легкого подъема тяжелых предметов. Таким образом, шестерни являются основным компонентом большинства оборудования, поскольку они довольно универсальны и способны выполнять множество задач.

В зависимости от профиля зубьев колес различают зацепления трех основных видов: эвольвентные, когда профиль зуба образован двумя симметричными эвольвентами; циклоидальные, когда профиль зубьев образован циклоидальными кривыми; зацепления Новикова, когда профиль зуба образован дугами окружности.

Две шестерни разных размеров заставят их две оси вращаться с разной скоростью, что очень важно в механических передачах. Это измерение помогает определить, насколько быстро механизм может двигаться в машине. Отношение числа зубьев колеса к числу зубьев шестерни называют передаточным числом. Зубчатое колесо, передающее вращение, называют ведущим, приводимое во вращение - ведомым. Колесо зубчатой пары с меньшим числом зубьев называют шестерней, сопряженное с ним парное колесо с большим числом зубьев - колесом.

Для чего используют шестерни ?

Шестерни очень полезный тип механизма, используемый для того, чтобы передать вращение от одной оси к другим. Их также можно использовать для увеличения / уменьшения скорости вращения, а также для изменения направления вращения. Скажем, у вас есть двигатель, который вращается со скоростью 100 оборотов в минуту, и вы хотите, чтобы он вращался только со скоростью 50 оборотов в минуту. Вы можете использовать систему шестерен, чтобы уменьшить скорость (а также увеличить крутящий момент), так что выходной вал вращается с «половинной» скоростью двигателя. Шестерни обычно работают в условиях высокой нагрузки, поэтому зубья шестерни должны быть спроектированы с высокой точностью и изготовлены из соответствующего материала. Это закладывается на этапе проектирования.

Элементы и характеристики зубчатого колеса.

Есть несколько различных терминов, которые необходимо знать, если вы только начинаете знакомиться с зубчатыми передачами. Для того чтобы шестерни сцепились, диаметральный шаг и угол давления должны быть одинаковыми.

Ось: ось вращения шестерни, где проходит вал.

Зубья: зубчатые грани, выступающие наружу от окружности шестерни, используемые для передачи вращения на другие шестерни. Число зубьев на шестерне должно быть целым числом. Шестерни передают вращение в том случае, если их зубья сцепляются и имеют одинаковый профиль.

Наружный диаметр. Это максимальный диаметр шестерни. Это расстояние от центра корпуса шестерни до вершины зуба. Внешний диаметр обозначает крайнюю протяженность шестерни.

Делительный диаметр для зубчатого колеса всегда один. Длина делительной окружности зубчатого колеса: πd = pt z (где π = 3,14), откуда диаметр делительной окружности d = (pt / π) z. Линейная величина, в π раз меньшая шага зацепления, называется модулем и обозначается буквой m.

Модуль зацепления называется иногда диаметральным шагом зубчатого колеса: отношение количества зубьев к диаметру шага. Две шестерни должны иметь одинаковый диаметральный шаг для зацепления. Введение модуля упрощает расчет и изготовление зубчатых передач, так как позволяет выражать различные параметры колеса (например, диаметры колеса) целыми числами, а не бесконечными дробями, связанными с числом п . ГОСТ 9563—60* установил следующие значения модуля, мм: 0,5; (0,55); 0,6; (0,7); 0,8; (0,9); 1; (1,125); 1,25; (1,375); 1,5; (1,75); 2; (2,25); 2,5; (2,75); 3; (3,5); 4; (4,5); 5; (5,5); 6; (7); 8; (9); 10; (11); 12; (14); 16; (18); 20; (22); 25; (28); 32; (36); 40; (45); 50; (55); 60; (70); 80; (90); 100.

Угол профиля исходного контура: угол давления шестерни - это угол между линией, определяющий радиус окружности шага до точки, где окружность шага пересекает зуб, и касательной к этому зубу в этой точке. Стандартные углы давления составляют 14,5, 20 и 25 градусов. Угол давления влияет на то, как шестерни контактируют друг с другом, и таким образом, как сила распределяется вдоль зуба. Две шестерни должны иметь одинаковый угол давления для зацепления.

Исходный контур. При стандартизации зубчатых колес и зуборезного инструмента для упрощения определения формы и размеров нарезаемых зубьев и инструмента введено понятие исходного контура. Это контур зубьев номинальной исходной зубчатой рейки в сечении плоскостью, перпендикулярной к ее делительной плоскости. На рисунке показан исходный контур по ГОСТ 13755—81 (СТ СЭВ 308—76) — прямобочный реечный контур со следующими значениями параметров и коэффициентов: угол главного профиля а = 20° ; коэффициент высоты головки h*a = 1 ; коэффициент высоты ножки h*f = 1,25 ; коэффициент радиуса кривизны переходной кривой р*f = 0,38 ; коэффициент глубины захода зубьев в паре исходных контуров h*w = 2 ; коэффициент радиального зазора в паре исходных контуров С* = 0,25 .

Для улучшения работы зубчатых колес (повышения прочности зубьев, плавности зацепления и тп.), получения заданного межосевого расстояния, во избежание подрезания зубьев и для других целей производят смещение исходного контура: положительное или отрицательное.

Для улучшения плавности работы цилиндрических колес (преимущественно при увеличении окружной скорости их вращения) применяют профильную модификацию зуба, в результате которой поверхность зуба выполняется с преднамеренным отклонением от теоретической эвольвентной формулы у вершины или у основания зуба. Например, срезают профиль зуба у его вершины на высоте hc = 0,45m от окружности вершин на глубину модификации А = (0,005%0,02) m

Различные типы шестерен

Существует множество различных типов шестерен и зубчатых механизмов. Вот некоторые из них: цилиндрическая зубчатая передача, косозубое колесо, зубчатая рейка, коническая шестерня, тангенциальная коническая передача, червячная передача, внутреннее зубчатое колесо и другие.

1. Цилиндрические зубчатые передачи

Цилиндрические зубчатые колеса самый простой тип шестерни. Зубчатые шестерни используются для того, чтобы перенести движение от одного вала к параллельному валу. Зубья расположены параллельно оси вращения. Когда два соседних зубчатых колеса сцепляются, они вращаются в противоположных направлениях. Эти шестерни наиболее часто используются, потому что они легко и быстро изготавливаются по сравнению с другими типами. Они отлично работают при умеренной нагрузке и умеренной скорости и обычно используются там, где шум и вибрация не являются проблемой. Другие типы шестерен требуют более точных и более сложных процедур обработки. Для изменения крутящего момента и числа оборотов можно использовать две прямозубые цилиндрические шестерни разного размера.Одним из его преимуществ является обеспечение высокого КПД трансмиссии при отсутствии осевой нагрузки на вал.

К некоторым недостаткам можно отнести высокий уровень шума и вибрации при работе на высоких скоростях, а также большую нагрузку на зубья в этой простой конструкции.

Зубчатой передачей называется механизм, служащий для передачи вращательного движения с одного вала на другой и изменения частоты вращения посредством зубчатых колес и реек.

Зубчатое колесо, сидящее на передающем вращение валу, называется ведущим, а на получающем вращение — ведомым. Меньшее из двух колес сопряженной пары называют шестерней; большее — колесом; термин «зубчатое колесо» относится к обеим деталям передачи.

Зубчатые передачи представляют собой наиболее распространенный вид передач в современном машиностроении. Они очень надежны в работе, обеспечивают постоянство передаточного числа, компактны, имеют высокий КПД, просты в эксплуатации, долговечны и могут передавать любую мощность (до 36 тыс. кВт).

К недостаткам зубчатых передач следует отнести: необходимость высокой точности изготовления и монтажа, шум при работе со значительными скоростями, невозможность бесступенчатого изменения передаточного числа.

В связи с разнообразием условий эксплуатации формы элементов зубчатых зацеплений и конструкции передач весьма разнообразны.

Зубчатые передачи классифицируются по признакам, приведенным ниже.

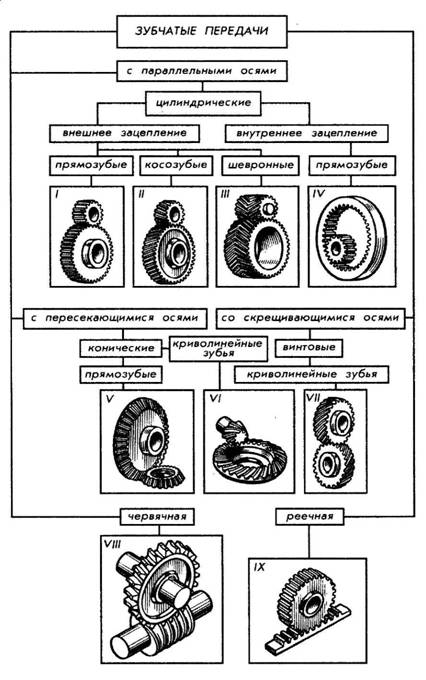
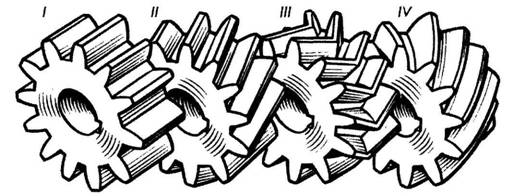
По взаимному расположению осей колес: с параллельными осями (цилиндрическая передача — рис. 172, I—IV); с пересекающимися осями (коническая передача — рис. 172, V, VI); со скрещивающимися осями (винтовая передача — рис. 172, VII; червячная передача — рис. 172, VIII).
В зависимости от относительного вращения колес и расположения зубьев различают передачи с внешним и внутренним зацеплением. В первом случае (рис. 172, I—III) вращение колес происходит в противоположных направлениях, во втором (рис. 172, IV) — в одном направлении. Реечная передача (рис. 172, IX) служит для преобразования вращательного движения в поступательное.
По форме профиля различают зубья эвольвентные (рис. 172, I, II) и неэвольвентные, например цилиндрическая передача Новикова, зубья колес которой очерчены дугами окружности.
В зависимости от расположения теоретической линии зуба различают колеса с прямыми зубьями (рис. 173, I), косыми (рис. 173, II), шевронными (рис. 173, III) и винтовыми (рис. 173, IV). В непрямозубых передачах возрастает плавность работы, уменьшается износ и шум. Благодаря этому непрямозубые передачи большей частью применяют в установках, требующих высоких окружных скоростей и передачи больших мощностей.
По конструктивному оформлению различают закрытые передачи, размещенные в специальном непроницаемом корпусе и обеспеченные постоянной смазкой из масляной ванны, и открытые, работающие без смазки или периодически смазываемые консистентными смазками (рис. 174).
По величине окружной скорости различают: тихоходные передачи (v равной до 3 м/с), среднескоростные (v равной от 3. 15 м/с) и быстроходные (v более 15 м/с).

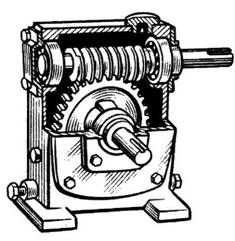
Основы теории зацепления

Боковые грани зубьев, соприкасающиеся друг с другом во время вращения колес, имеют специальную криволинейную форму, называемую профилем зуба. Наиболее распространенным в машиностроении является эвольвентный профиль (рис. 175).

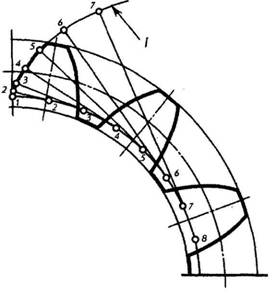
Придание профилям зубьев зубчатых зацеплений таких очертаний не является случайностью. Чтобы зубья двух колес, находящихся в зацеплении, могли плавно перекатываться один по другому, необходимо было выбрать такой профиль для зубьев, при котором не происходило бы перекосов и защемления головки одного зуба во впадине другого.

На рис. 176 изображена пара зубчатых колес, находящихся в зацеплении. Линия, соединяющая центры колес О₁ и О₂ называется линией центров или межосевым расстоянием — a_w.

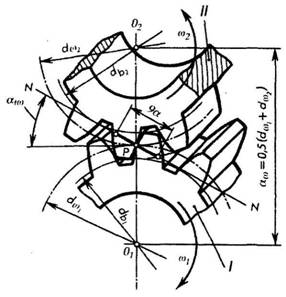
Точка Р касания начальных окружностей d_W₁ и d_W₂ — полюс — всегда лежит на линии центров. Начальными называются окружности, касающиеся друг друга в полюсе зацепления, имеющие общие с зубчатыми колесами центры и перекатывающиеся одна по другой без скольжения.

Если проследить за движением пары зубьев двух колес с момента, когда они впервые коснутся друг друга до момента, когда они выйдут из зацепления, то окажется, что все точки касания их в процессе движения будут лежать на одной прямой NN. Прямая NN, проходящая через полюс зацепление Р и касательная к основным* окружностям db₁, db₂, двух сопряженных колес, называется линией зацепления. Отрезок g_a линии зацепления, отсекаемый окружностями выступов сопряженных колес, — активная часть линии зацепления, определяющая начало и конец зацепления пары сопряженных зубьев.

Линия зацепления представляет собой линию давления сопряженных профилей зубьев в процессе эксплуатации зубчатой передачи.

Угол ?_w между линией зацепления и перпендикуляром к линии центров O₁О₂ называется углом зацепления. В основу профилирования эвольвентных зубьев и инструмента для их нарезания положен стандартный по ГОСТ 13755-81 исходный контур так называемой рейки, равный 20°.

Во время работы цилиндрической прямозубой передачи сила давления Р_n ведущей шестерни O₁ в начале зацепления передается ножкой зуба на сопряженную боковую поверхность (контактную линию) головки ведомого колеса О₂. Чем больше пара зубьев одновременно находится в зацеплении, тем более плавно работает передача, тем меньшую нагрузку воспринимает на себя каждый зуб.

Стремление сделать зубчатую передачу более компактной вызывает необходимость применять зубчатые колеса с возможно меньшим числом зубьев. Изменение количества зубьев зубчатого колеса влияет на их форму (рис. 177). При увеличении числа зубьев до бесконечности колесо превращается в рейку и зуб приобретает прямолинейное очертание. С уменьшением числа зубьев одновременно уменьшается толщина зуба у основания и вершины, а также увеличивается кривизна эвольвентного профиля, что приводит к уменьшению прочности зуба на изгиб. При уменьшении числа зубьев, когда z < z_mim, происходит так называемое подрезание зубьев, то есть явление, когда зубья большого колеса при вращении заходят в область ножки меньшего колеса (см. заштрихованная площадь на рис. 177), тем самым ослабляя зуб в самом опасном сечении, увеличивая износ зубьев и снижая КПД передачи.

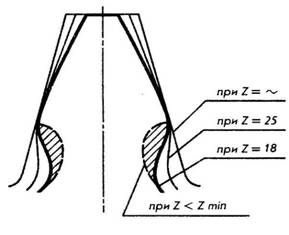
На практике подрезку зубьев предотвращают прежде всего выбором соответствующего числа зубьев. Наименьшее число зубьев (z_min), при котором еще не происходит подрезание, рекомендуется выбирать от 35 до 40 при равном 15° и от 18 до 25 при ?_w равном 20°.

В отдельных случаях приходится выполнять передачу с числом зубьев меньшим, чем рекомендуется, при этом производят исправление, или, как говорят, корригирование формы зубьев. Один из таких способов заключается в изменении высоты головки и ножки зуба до h_a = 0,8m; h_f = m. Этот способ исключает подрезку, но увеличивает износ зубьев.

Теперь обратимся к изложению основной теоремы зацепления: общая нормаль (линия зацепления NN) к сопряженным профилям зубьев делит межосевое расстояние ( ?_w= О₁О₂) на отрезки (О₁Р и 0₂Р), обратно пропорциональные угловым скоростям (w₁ и w₂). Если положение точки Р (полюса зацепления) неизменно в любой момент зацепления, то передаточное отношение — отношение частоты вращения ведущего колеса к частоте вращения ведомого — будет постоянным.

4.3. Основные элементы зубчатых зацеплений. При изменении осевого расстояния ?_w = О₁О₂ пары зубчатых колес будет меняться и положение полюса зацепления Р на линии центров, а следовательно, и величина диаметров начальных окружностей, то есть у пары сопряженных зубчатых колес может быть бесчисленное множество начальных окружностей. Следует отметить, что понятие начальные окружности относится лишь к паре сопряженных зубчатых колес. Для отдельно взятого зубчатого колеса нельзя говорить о начальной окружности.

Если заменить одно из колес зубчатой рейкой, то для каждого зубчатого колеса найдется только одна окружность, катящаяся по начальной прямой рейке без скольжения, — эта окружность называется делительной.

Примечание. В настоящей книге рассматриваются зубчатые передачи, у которых начальные и делительные окружности совпадают.

Так как у каждого зубчатого колеса имеется только одна делительная окружность, то она и положена в основу определения основных параметров

зубчатой передачи по ГОСТ 16530- 83 и ГОСТ 16531-83 (рис. 178)

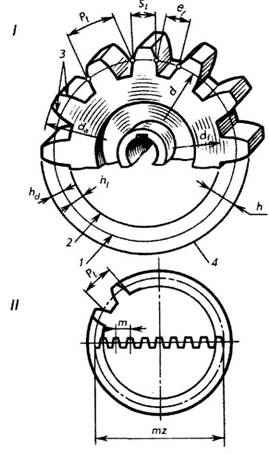
Основные параметры зубчатых колес:

1. Делительными окружностями пары зубчатых колес называются соприкасающиеся окружности, катящиеся одна по другой без скольжения. Эти окружности, находясь в зацеплении (в передаче), являются сопряженными. На чертежах диаметр делительной окружности обозначают буквой d.

2. Окружной шаг зубьев Р_t — расстояние (мм) между одноименными профильными поверхностями соседних зубьев. Шаг зубьев, как нетрудно представить, равен делительной окружности, разделенной на число зубьев z.

3. Длина делительной окружности. Модуль. Длину делительной окружности можно выразить через диаметр и число зубьев: Пd = P_t • r. Отсюда диаметр делительной окружности d = (Рt • z)/П.

Отношение P_t/П называется модулем зубчатого зацепления и обозначается буквой т. Тогда диаметр делительной окружности можно выразить через модуль и число зубьев d = m • z. Отсюда m = d/z.

Значение модулей для всех передач — величина стандартизированная.

Для понимания зависимости между величинами Р_t т и d приведена схема на рис. 178, II, где условно показано размещение всех зубьев 2 колеса по диаметру ее делительной окружности в виде зубчатой рейки.

4. Высота делительной головки зуба h_a — расстояние между делительной окружностью колеса и окружностью вершин зубьев.

5. Высота делительной ножки зуба h_f — расстояние между делительной окружностью колеса и окружностью впадин.

6. Высота зуба h — расстояние между окружностями вершин зубьев и впадин цилиндрического зубчатого колеса h = h_a + h_f_..

7. Диаметр окружности вершин зубьев d_a — диаметр окружности, ограничивающей вершины головок зубьев.

8. Диаметр окружности впадин зубьев d_f — диаметр окружности, проходящей через основания впадин зубьев.

При конструировании механизма конструктор рассчитывает величину модуля т для зубчатой передачи и, округлив, подбирает модуль по таблице стандартизированных величин. Затем он определяет величины остальных геометрических элементов зубчатого колеса.

Зубчатые передачи с зацеплением M.Л. Новикова

В этом зацеплении профиль зубьев выполняется не по эвольвенте, а по дуге окружности или по кривой, близкой к ней (рис. 179).

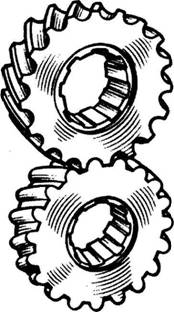
При зацеплении выпуклые зубья одного из колес контактируют с вогнутыми зубьями другого. Поэтому площадь соприкосновения одного зуба с другим в передаче Новикова значительно больше, чем в эвольвентных передачах. Касание сопряженных профилей теоретически происходит в точке, поэтому данный вид зацепления называют точечным.

При одинаковых с эвольвентным зацеплением параметрах точечная система зацепления с круговым профилем зуба обеспечивает увеличение контактной прочности, что в свою очередь позволяет повысить нагрузочную способность передачи в 2. 3 раза по сравнению с эвольвентной. Взаимодействие зубьев в сравниваемых передачах также различно: в эвольвентном зацеплении преобладает скольжение, а в зацеплении Новикова — качение. Это создает благоприятные условия для увеличения масляного слоя между зубьями, уменьшения потерь на трение и увеличения сопротивления заеданию.

К достоинствам зацепления Новикова относятся возможность применения его во всех видах зубчатых передач: с параллельными, пересекающимися и скрещивающимися осями колес, с внешним и внутренним зацеплением, постоянным и переменным передаточным отношением. Потери на трение в этой системе зацепления примерно в 2 раза меньше потерь в эвольвентном зацеплении, что увеличивает КПД передачи.

К основным недостаткам передач с зацеплением Новикова относятся: технологическая трудоемкость изготовления колес, ширина колес должна быть не менее 6 модулей и др. В настоящее время передачи с зацеплением Новикова находят применение в редукторах больших размеров.

Читайте также: