Что такое точка обода колеса

Опубликовано: 14.05.2024

На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.

В то же время из школьного курса математики известно, что длина окружности равна:

Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.

Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:

C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.

Но на самом деле она проходит фактически путь вдвое больший.

Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.

Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.

Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.

Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.

Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:

V = w*R, где w - угловая скорость вращения колеса.

Фактически линейная скорость внутренних точек колеса должна описываться уравнением:

V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.

Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.

Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.

Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:

dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R

Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.

С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.

Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.

[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.

Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.

Сазонов Сергей 3 сентября 2019 года в 12:54

Писать рецензию на Вашу бредятину "Парадокс колеса" считаю излишним (много чести) - найдите в детском журнале "Квант" за 1975 год статью "ЦИКЛОИДА" . Там - примерно этот круг вопросов. Парадокса нет.
(конец цитаты)

К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.

Детская задача. Парадокса нет - обод внутреннего колеса будет принудительно протаскивается со скольжением, если внутреннее будет катится по гладкому рельсу, а внешнее будет катиться по зубчатому для устранения скольжения.
Задача механическая, а не геометрическая. А так она изложена на манер задачи "Догонит ли Ахиллес черепаху?".
Вот вам встречный парадокс - "Что такое настоящее время?". Можно ли его поймать и зафиксировать в цифрах на носителе? И какой промежуток занимает это "Настоящее" между Прошлым и Будущим временами?
Таких парадоксов у меня накопилось не мало. А решения нет.

Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.

Ежедневная аудитория портала Проза.ру – порядка 100 тысяч посетителей, которые в общей сумме просматривают более полумиллиона страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.

Что общего между вращением Земли вокруг своей оси, движением стрелок часов, колес автомобиля на прямолинейном участке пути и т. п.? С точки зрения кинематики, все это примеры так называемого плоскопараллельного движения твердого тела, при котором все точки тела перемещаются в параллельных плоскостях.

Разумеется, в самом общем случае различные точки тела могут двигаться по-разному. Однако принято выделять два частных случая и говорить о двух простейших типах движения — о поступательном движении и о вращении вокруг неподвижной оси. В первом случае все точки тела совершают одинаковые перемещения. Это движение самое простое, и здесь мы его обсуждать не будем. Во втором случае все точки описывают одинаковые траектории — окружности с центрами на оси вращения. Основной характеристикой такого движения является угловая скорость вращения ω.

Давайте вычислим, например, угловые скорости стрелок часов. Так как стрелки вращаются равномерно, то угол поворота φ со временем изменяется по закону φ = ωt (уравнение равномерного вращения). Секундная стрелка делает один оборот за 60 секунд; следовательно, ее угловая скорость равна ω_с = 2π / 60 с = 0,1047 с -1 . Аналогично, скорость часовой стрелки равна ω_ч = 2π / (12·60·60) с = 0,0001455 с -1 .

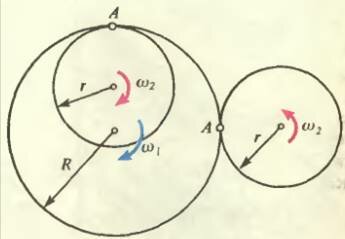
А как добиться того, чтобы секундная и часовая стрелки двигались с различными угловыми скоростями, но синхронно? Оказывается, для этого используется зубчатая передача: два зубчатых колеса могут вращаться вокруг разных осей, но при этом они входят в зацепление друг с другом (рис. 1). Поскольку линейные скорости точки А одинаковы —

\upsilon_A = \omega_1 R = \omega_2 r\) ,

где z₁ и z₂ — число зубцов шестеренок.

Кроме того, можно заметить, что при внутреннем зацеплении вращение шестеренок происходит в одном направлении, а при внешнем — в противоположных направлениях. С помощью таких (и более сложных) зубчатых передач осуществляется соединение стрелок в часах, передача усилий в домкрате, изменение величины скорости и «задний ход» у автомобиля.

Теперь рассмотрим более сложное плоскопараллельное движение твердого тела, когда тело вращается, но ось вращения сама поступательно перемещается в пространстве. Скорости такого движения проще всего найти, используя понятие мгновенного центра вращения — так называют точку, скорость которой в данный момент времени равна нулю. Скорости всех остальных точек тела при этом будут такими, как будто тело вращается вокруг неподвижной оси, проходящей через мгновенный центр вращения.

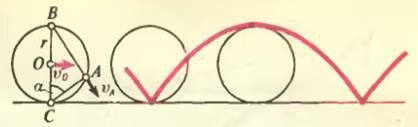
В качестве примера разберем движение колеса на прямолинейном участке пути без проскальзывания. Так как колесо не проскальзывает, точка С (рис. 2), в которой колесо касается дороги, имеет скорость равную нулю. Значит, точка С и есть мгновенный центр вращения. Найдем, какой будет угловая скорость вращения колеса, если скорость его центра О (скорость поступательного движения колеса) равна υ₀:

\upsilon_0 = \omega r\) , и \(

Легко находится и скорость произвольной точки А. Она направлена по линии АВ и равна

\upsilon_A = \omega \cdot CA = 2 \omega r \cos \alpha = 2 \upsilon_0 \cos \alpha\) .

На рисунке 2 изображена также траектория, которую описывает каждая точка обода катящегося колеса. Эта удивительная кривая — циклоида — встретится вам во многих случаях: по такой траектории движутся частицы в «скрещенных» (взаимно перпендикулярных) электрическом и магнитном полях, по циклоиде шарик скатывается за минимальное время и т. д.

Теперь легко ответить на вопрос, который обычно вызывает затруднения: почему, если смотреть на движущегося велосипедиста, то верхние спицы колес сливаются в одно целое, а нижние видны раздельно. Очевидно, это связано с тем, что скорости нижней половины колеса меньше, чем верхней (подумайте, почему, если смотреть на велосипедиста из окна движущегося в ту же сторону автобуса, этот эффект пропадает?).

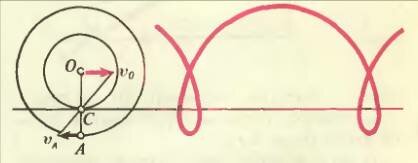
А что если мы захотим определить скорость колес вагона движущегося поезда? Мы обнаружим, что на ободе колеса имеются точки, которые движутся назад, в противоположную движению поезда сторону. Это — точки выступающей части колеса, например точка А на рисунке 3. Мгновенный центр вращения (точка С) находится на неподвижном рельсе, по которому колесо катится без проскальзывания. Траектория точки обода колеса еще более любопытна, чем в предыдущем случае,— на траектории имеются возвратные участки движения (петли). Интересно отметить, что аналогичные петлеобразные траектории описывают в своем движении планеты. Их наблюдали еще древнегреческие астрономы, однако объяснить увиденное они не смогли. Сейчас мы знаем, что эти траектории связаны с наложением двух вращений — Земли и наблюдаемой планеты вокруг Солнца.

Всегда ли при плоскопараллельном движении траектории оказываются такими сложными? Попробуйте определить, например, какую траекторию описывают точки обода колеса радиусом r, которое катится по внутренней поверхности неподвижного колеса радиусом 2r.

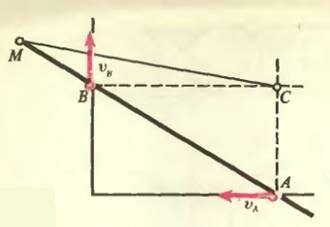
В заключение мы хотим познакомить вас с простым по конструкции, но важным для практики прибором — линейкой-эллипсографом (рис. 4), который служит для вычерчивания эллипсов. Точки А и В такого прибора двигаются по взаимно перпендикулярным направляющим ОА и OB, a точка М при этом описывает эллипс (подумайте, почему). Где находится мгновенный центр вращения в этом случае? Как найти скорость точки М, зная скорости точек А и В?

Рассмотрим жесткий треугольник СВА (точка С лежит на пересечении перпендикуляров к направляющим). Проекции скоростей двух точек твердого тела на линию их соединения всегда равны. Для точек С, А и С, В это возможно, если υ_C, т. е. если точка С — мгновенный центр вращения. Скорость точки М можно определить, зная скорость точки А, например:

\upsilon_A = \omega \cdot CA\) , и \(

\upsilon_M = \upsilon_A \cdot \frac\) .

Аналогичным образом, используя понятие мгновенного центра вращения, можно легко находить скорости любых точек механизмов, совершающих плоскопараллельное движение.

alt="Лицензия Creative Commons" width="" />

Загадка тележного колеса

Прикрепите сбоку к ободу тележного колеса (или к шине велосипедного) цветную бумажку и наблюдайте за ней во время движения телеги (или велосипеда). Вы заметите странное явление: пока бумажка находится в нижней части катящегося колеса, она видна довольно отчетливо; в верхней же части она мелькает так быстро, что вы не успеваете ее разглядеть.

Выходит как будто, что верхняя часть колеса движется быстрее, чем нижняя. То же наблюдение можно сделать, если сравнить между собой верхние и нижние спицы катящегося колеса какого-нибудь экипажа. Будет заметно, что верхние спицы сливаются в одно сплошное целое, нижние же видимы раздельно. Дело опять-таки происходит так, словно верхняя часть колеса быстрее движется, чем нижняя.

В чем же разгадка этого странного явления? Да просто в том, что верхняя часть катящегося колеса действительно движется быстрее, чем нижняя. Факт представляется с первого взгляда невероятным, а между тем простое рассуждение убедит нас в этом. Ведь каждая точка катящегося колеса совершает сразу два движения: обращается вокруг оси и в то же время подвигается вперед вместе с этой осью. Происходит сложение двух движений, и результат для верхней и нижней частей колеса получается разный. Вверху вращательное движение колеса прибавляется к поступательному, так как оба движения направлены в одну и ту же сторону. Внизу же вращательное движение направлено в обратную сторону и, следовательно, отнимается от поступательного. Вот почему верхние части колеса перемещаются относительно неподвижного наблюдателя быстрее, чем нижние.

Итак, не все точки движущегося колеса телеги перемещаются одинаково быстро. Какая же часть катящегося колеса движется всего медленнее?

Нетрудно сообразить, что медленнее всех движутся те точки колеса, которые в данный момент соприкасаются с землей. Строго говоря, в момент соприкосновения с почвой эти точки колеса совершенно неподвижны.

Все сказанное справедливо только для колеса катящегося, а не для такого, которое вращается на неподвижной оси. В маховом колесе, например, верхние н нижние точки обода движутся с одинаковой скоростью

В этой статье мы рассмотрим основную часть велосипедного колеса – обод. На рисунке с поперечным сечением колеса это 1. Так же упомянем и об ободной ленте (номер 2 на рисунке), для чего она нужна.

Что такое обод? Согласно Википедии – это наружная часть колеса в виде круга, которая крепится к ступице колеса (втулке) на натянутых спицах.

Обод – это основа колеса и поэтому он должен быть:

Прочным;
Жестким;
Легким.

Прочность и жесткость.

Обе эти характеристики определяются материалом, из которого сделан обод и формой профиля. Причем профиль даже более важен, чем материал.

Легкость

Насчет легкости. Это важно не только с точки зрение переноса байка велосипедистом, но и с точки зрения езды на нем. Чем легче велосипед – тем проще его разогнать. Причем есть закономерность – грамм веса в колесе требует в два раза больше энергии, чем тот же грамм в раме или других элементах. Это нужно обязательно учитывать.

Из чего изготавливают обода

Обода изготавливают в основном из следующих материалов:

Сталь.
Алюминиевые сплавы.
Карбон.

Сегодня большинство колес собирают на основе ободов изготовленных из алюминиевых сплавов. Колеса ни их основе легче стальных, а благодаря специальной форме профиля их жесткость даже выше. Для повышения прочности алюминиевые обода проходят еще и термическую обработку, так называемую закалку, а после этого анодирование и покраску, что делает их еще более устойчивыми к коррозии. При всех плюсах и у них есть минус. Алюминиевые колеса – все же дороже стальных.

Изготавливают современные обода методом экструзии. Это когда полу расплавленный металл выдавливают через отверстие, определяющее поперечное сечение обода. Затем полученный профиль изгибается в ровное кольцо и скрепляется при помощи сварки.

Карбоновые обода очень легкие и прочные, но уж очень дороги. Их изготавливают вместе со спицами. На рисунке выше как раз образец такого обода с пятью спицами.

Тип и профиль обода

Как было описано обода в основном изготавливают из стали и алюминия. Жесткость и прочность обода во многом зависит не только от материала, но и от вида профиля, из которого его изготовляют.

Обода бывают одинарные, двойные, тройные.

Одинарные

Одинарные обода изготавливают, в основном, из стали. Это самый простой и дешевый вариант. Их используют на городских велосипедах, не испытывающих сильных ударных нагрузок и предназначенных для спокойной езды или детских моделях. Причем это всегда модели с ножными барабанными тормозами.

Двойные

Двойными они называются потому, что кроме нижней стенки, к которой крепятся спицы, есть еще и вторая перегородка. Именно за счет второй перегородки такие обода имеют высокую прочность и жесткость. Двойные обода устанавливают на большинство байков среднего и высокого класса. Изготавливают их из алюминиевых сплавов, что обеспечивает малый вес и высокие антикоррозийные свойства.

Тройные

Это наиболее прочные, но, в тоже время, и самые тяжелые обода. Встречаются довольно редко. Дополнительная перемычка предназначена для повышения боковой прочности при использовании мощных ободных тормозов. Однако на сегодняшний день такие тормоза все более вытесняются дисковыми тормозами, а для них такие мощные обода не нужны, так как для торможения используется тормозной диск (ротор), а не сдавливание обода. С точки зрения жесткости, такие обода применяются только в экстремальных видах велоспорта, так что они не очень сильно распространены.

Обода для бескамерных покрышек

Существуют еще и специальные обода для бескамерных покрышек.

Первая технология: UST (Universal System Tubeless) универсальная бескамерная система, разработанный в 1999 году французской компанией Mavic.

Второй вариант - технология BST (Bead Socket Technology), фирмы Stan’s, позволила устанавливать бескамерку практически на любое велосипедное колесо.

Высота обода

Если необходим обод с большей прочностью, то применяется высокий профиль. Это значительно повышает его жесткость и прочность «на складывание». Такому колесу менее страшны кочки и ямы на дороге или гоночной трассе.

Чем выше профиль обода, тем лучше он держит фронтальные удары, чем шире обод, тем больше его торсионная жесткость.
Обо да для стрита и фрирайда имеют довольно высокий профиль и ширину. здесь хватает ударов со всех сторон. В стрите и триале чаще используют обода с коробчатым профилем.

Зависимость от типа тормоза

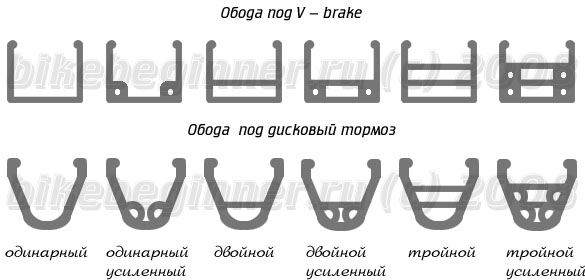
Как Вы уже поняли, тип используемого обода во многом определяется еще и типом тормоза, установленного на велосипеде.

На байках с тормозами типа V-brake ставят алюминиевые обода с ровной боковой стенкой. Причем на дорогих и качественных ободах протачивают специальную канавку, предназначенную для контроля износа боковых стенок. Как только ее не будет видно – обод нужно менять. Например на рисунке изображены высокие двойные алюминиевые обода.

При использовании дисковых тормозов широкие боковые стенки использовать не обязательно, поэтому их делают более узкими. Естественно, обода, предназначенные для использования на велосипедах с дисковыми тормозами, из-за отсутствия тормозных дорожек, не могут использоваться с ободными тормозами, а наоборот можно.

Керамические обода

Так называют обода со специальным керамическим покрытием на тормозных дорожках при использовании вибрейк тормозов. Толщина слоя - менее 1 мм.

Плюсы керамических ободов:

Резко возрастает эффективность работы тормоза не только в хорошую погоду, но и под дождем, снегом, в грязи.
Керамика очень жесткая и практически не стирается при эксплуатации.

Минусы керамических тормозных дорожек:

Обода с керамическим покрытием значительно дороже. К ним нужны специальные более жесткие тормозные колодки.
Высокая вероятность скола покрытия при агрессивном катании.

Сам обод значительно мягче керамического покрытия и постоянно испытывает деформации от нагрузок при катании и перепадов температур. Жесткой керамике такое выдержать сложно и уже через 2-3 года она начинает трескаться и отслаиваться.

Причем, самое обидное, что обод целый и крепкий, а нормально тормозить уже нельзя. Особенно это заметно при частых ударах по колесу и при появлении «восьмерок».

Лучше всего их использовать на асфальте и ровном грунте. Горные каменистые склоны и лесные тропинки керамика может не выдержать.

Пистонирование ободов

Смысл этого термина в следующем. В колесе спицы натягиваются между ободом и втулкой. При этом они работают на натяжение. В месте крепления спицы к ободу накапливается усталость металла, он может трескаться, что приведет к вырыванию спицы.

Для того, чтобы избежать этого используют пистонирование. Каждую спицу устанавливают в специальный стакан в ободе – пистон, который распределяет нагрузку, увеличивая ресурс колеса. Бывают еще и резьбовые пистоны, которые вкручиваются во внешнюю стенку обода, а внутренняя стенка не сверлится вообще.

Правда иногда никакое пистонирование не помогает. На фотографии видно к чему приводит сильное перетягивание спиц и слишком агрессивная езда.

Ободная лента

Ободная лента это резиновая или полимерная лента, защищающая камеру от проколов со стороны обода спицами или острыми концами отверстий для спиц. Так же она позволяет герметизировать обод.

Более подробно о ней можно почитать в соответствующей статье на нашем сайте.

Рис. 3.2. Циклоида как траектория точки обода катящегося колеса

Циклоиду можно рассматривать как траекторию какой-либо точки обода колеса, которое катится без проскальзывания по прямой. На рис. 3.2 показана циклоида, которую «вычерчивает» точка 𝐴, находившаяся внизу в начальный момент. Точка 𝐴 описывает данную циклоиду независимо от того, катится ли колесо равномерно или с ускорением, важно только, чтобы оно не проскальзывало. Проще всего рассмотреть, разумеется, равномерное качение колеса. Такое качение получается в результате сложения равномерного вращения колеса вокруг оси и равномерного поступательного движения, линейная скорость которого 𝑣 равна произведению угловой скорости на радиус колеса 𝑟.

Во всех инерциальных системах отсчёта материальная точка имеет одно и то же ускорение. Поэтому находить его можно в любой такой системе отсчёта. Ясно, что ускорение точек обода колеса связано только с его вращением вокруг оси. Поэтому ускорение 𝑎 любой точки обода направлено по радиусу к центру колеса и определяется выражением

Значит, и в высшей точке циклоиды ускорение элемента обода колеса равно 𝑣²/𝑟 и направлено вниз (рис. 3.2).

Теперь рассмотрим движение этой же точки обода как движение по циклоиде. Скорость в любой точке траектории направлена по касательной к ней; значит, в высшей точке циклоиды скорость направлена горизонтально. Ускорение же, как мы выяснили, направлено вертикально вниз, т.е. перпендикулярно скорости. Поэтому найденное выше ускорение может быть записано также в виде

где 𝑉 - скорость точки обода в её верхнем положении, а 𝑅 - искомый радиус кривизны циклоиды.

Для нахождения 𝑉 будем рассуждать следующим образом. Скорость любой точки обода катящегося колеса равна векторной сумме скорости поступательного движения колеса и линейной скорости вращения вокруг оси. При отсутствии проскальзывания эти скорости равны по модулю. В верхней точке они и направлены одинаково. Поэтому 𝑉=2𝑣, и, сравнивая формулы (1) и (2), находим

Радиус кривизны циклоиды в верхней точке равен удвоенному диаметру колеса. Если бы мы рассматривали качение колеса как вращение вокруг мгновенной оси, совпадающей в каждый момент с нижней неподвижной точкой колеса (рис. 3.2), то могло бы показаться, что верхняя точка движется по окружности, радиус которой равен диаметру колеса. Так оно и было бы, если бы мгновенная ось вращения 𝑂 оставалась неподвижной. На самом деле эта ось перемещается вместе с колесом, и именно поэтому рассматриваемая точка обода 𝐴 движется в этот момент по окружности, радиус которой даётся формулой (3). ▲

4. Падающий мяч.

Заброшенный в кольцо баскетбольный мяч начинает отвесно падать из корзины без начальной скорости. В тот же момент из точки, находящейся на расстоянии 𝑙 от кольца, в падающий мяч бросают теннисный мяч (рис. 4.1). С какой начальной скоростью был брошен теннисный мяч, если мячи столкнулись на расстоянии ℎ от кольца?

Рис. 4.1. Падающий мяч

△ В поставленном вопросе подразумевается, что нужно найти вектор начальной скорости теннисного мяча, т.е. его направление (угол α) и модуль (𝑣₀). Если решать задачу в исходной (лабораторной) системе отсчёта, то ход рассуждений может быть следующим. Записываем выражения для перемещений обоих мячей за время 𝑡 от начала движения до их встречи, затем проецируем их на вертикальное и горизонтальное направления (рис. 4.2). В результате приходим к системе уравнений

Здесь 𝐻 - высота кольца над точкой бросания теннисного мяча, а √𝑙²-𝐻² представляет собой расстояние до кольца по горизонтали (рис. 4.2).

Рис. 4.2. Проекции перемещений мячей

В системе трёх уравнений (1) четыре неизвестных величины: 𝑣₀, α, 𝑡 и 𝐻. Поэтому может показаться, что задача не имеет единственного решения. Однако это не так. Действительно, подставляя ℎ из первого уравнения во второе, получаем

Разделив почленно это уравнение на третье уравнение системы (1), находим выражение для tg α:

Теперь с помощью рис. 4.2 можно увидеть, что угол α, под которым должна быть направлена начальная скорость теннисного мяча, в действительности соответствует направлению из точки бросания на кольцо. Истинное направление начальной скорости 𝒗₀ показано на рис. 4.3. Итак, бросать теннисный мяч нужно точно в направлении кольца. Модуль его начальной скорости можно найти, подставляя 𝑡=√2ℎ/𝑔 из первого уравнения системы (1) в уравнение (2). Учитывая, что 𝐻/sin α=𝑙, получаем

Рис. 4.3. Истинное направление вектора 𝑣₀ начальной скорости

Но всех этих преобразований можно избежать, если с самого начала перейти в систему отсчёта, связанную с баскетбольным мячом, т.е. свободно падающую с ускорением 𝒈 в этой системе отсчёта баскетбольный мяч, естественно, неподвижен, а теннисный движется равномерно и прямолинейно со скоростью 𝒗₀. Очевидно, что эта скорость 𝒗₀ должна быть направлена на баскетбольный мяч. Через время 𝑡=𝑙/𝑣₀ мячи столкнутся. В лабораторной системе отсчёта за это время баскетбольный мяч опустится на расстояние

откуда для 𝑣₀ получаем прежнее выражение (4). На примере этой задачи мы видим, что в некоторых случаях удобным оказывается переход в ускоренно движущуюся систему отсчёта. ▲

5. В цель с наименьшей начальной скоростью.

Необходимо с поверхности земли попасть камнем в цель, которая расположена на высоте ℎ и на расстоянии 𝑠 по горизонтали. При какой наименьшей начальной скорости камня это возможно? Сопротивлением воздуха пренебречь.

△ На первый взгляд кажется, что начальная скорость камня будет наименьшей, если верхняя точка его траектории совпадает с мишенью (рис. 5.1а).

Рис. 5.1. К выбору оптимальной траектории

Может быть, и вам так показалось? Иллюзия эта настолько сильна, что подобное решение аналогичной задачи можно встретить в некоторых солидных пособиях по решению физических задач. Однако, даже не решая задачи, легко убедиться, что это не так. Действительно, будем мысленно уменьшать высоту, на которой расположена цель. При этом точка, куда попадает камень, продолжает согласно предположению оставаться верхней точкой траектории (рис. 5.1б), в том числе и в предельном случае ℎ=0. Но совершенно очевидно, что для того чтобы попасть в цель, находящуюся на земле, достаточно просто добросить камень до цели (рис. 5.1б). Итак, предположение о том, что цель совпадает с высшей точкой траектории полёта камня, неверно.

Читайте также: